Before writing a parser for a regular expression language, one needs to define the rules of the language, or grammar. When you learn a new (programming) language, like Swift or Regex, you typically go through a guide written in a natural language like English. This is a great way to learn a language, but it’s not the optimal way to describe it.
Note. This article outlines some of the theory behind languages and grammars. If that’s not what you are interested in, you can skip it and jump straight into parsing. I would still recommend revisiting this article later.
The syntaxes of most programming languages in use today are defined through formal grammars. If you’ve opened the Swift Language Reference before, you’ve probably seen the blocks like this:
Grammar of Structure Declaration
struct-declaration → attributesopt access-level-modifieropt struct struct-name generic-parameter-clauseopt type-inheritance-clauseopt generic-where-clauseopt struct-body
struct-name → identifier
struct-body → { struct-membersopt }
struct-members → struct-member struct-membersopt
struct-member → declaration | compiler-control-statement
This is an example of a formal grammar described using a special notation. It might seem a bit scary at first, like any unfamiliar mathematical notation does. But bear with me. By the end of this article you are going to learn what formal grammars are, why you need them, and how to read and write different formal grammar notations. Finally, we will define a subset of a regular expression language grammar using an Extended Backus-Naur form (EBNF).
Grammar #
What exactly is grammar? The term comes from the linguistics, which is the scientific study of language. If you ever studied a foreign language, you know that grammar consists of rules that describe the language. For example, English grammar contains rules like this:
Adjective can modify nouns. An adjective can be put before the noun.
A formal linguist or a computer scientist would describe this rule using a formal, generative grammar:
ModifiedNoun ::= Adjective Noun | Adjective ", " ModifiedNoun
Adjective ::= "fast" | "blue"
Noun ::= "car" | "sky"
A diagram generated using Railroad Diagram Generator for this grammar:
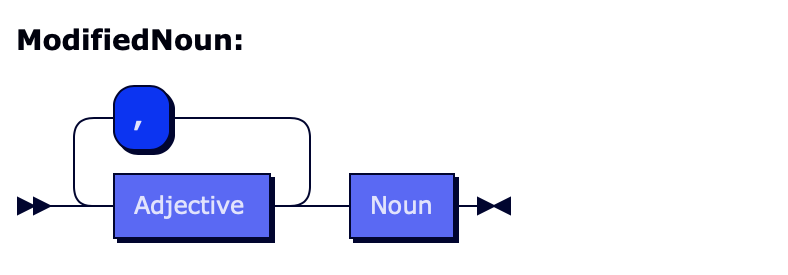
But what does it mean for grammar to be generative? You can think of a generative grammar as a recipe for constructing sentences in the language. Let’s see an example. You start with ModifiedNoun – it’s the first symbol on the list. Then you begin substituting:
ModifiedNoun // Start
Adjective Noun // Select the first alternative
fast Noun // Substitute Adjective
fast car // Substitute Noun
That was easy. What happens if you substitute another noun?
fast sky
Hmm, this doesn’t make any sense! But this is fine. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form.
The first option of ModifiedNoun was simple, but the other one is defined using ModifiedNoun itself! This is a recursive symbol. Namely, it is right-recursive because a non-terminal symbol ModifiedNoun appears on the right side.
ModifiedNoun // Start
Adjective, ModifiedNoun // Select the second alternative
fast, ModifiedNoun // Substitute Adjective
fast, Adjective Noun // Select the first alternative
fast, blue Noun // Substitute Adjective
fast, blue car // Substitute Noun
Awesome! We just saw a recursive production rule in action. I’ve used a few new terms in this section: non-terminal, production rule, etc. I think it’s time to formally define “formal grammar”.
Formal Grammar #
In the formalization of generative grammars first proposed by Noam Chomsky in the 1950s, a grammar G is defined the following way:
A grammar is formally defined as the tuple
(N, Σ, P, S):
- A finite set
Nof non-terminal symbols- A finite set
Σof terminal symbols that is disjoint fromN- A finite set
Pof production rules- A start symbol
S
Terminal symbols are literal symbols which cannot be changed using the rules. After you finish applying all the rules, it terminates with an output string which consists only of terminal symbols, e.g. Adjective in the production rule:
Adjective ::= "fast" | "blue"
Non-terminal symbols are those symbols which should be replaced, e.g. ModifiedNoun in the production rule:
ModifiedNoun ::= Adjective Noun | Adjective, ModifiedNoun`
Chomsky Hierarchy (Additional Reading)
In the 1950s, Noan Chomsky created a hierarchy of grammars. There are four categories of formal grammars in the Chomsky Hierarchy, spanning from Type 0, the most general, to Type 3, the most restrictive. Each layer is different in terms of the restriction applied to the production rules, the class of language it generates, the type of automaton that recognizes it.
Most programming languages are defined using Type 2 grammars, or Context-Free Grammars (CFG). In context-free grammars, all production rules must have only one (non-terminal) symbol on the left-hand side. It essentially means that regardless in which context the non-terminal symbol appears, it should be also interpreted the same way. Context-free grammars can be recognized using pushdown automata.
Another important type is Type 3 which describes Regular Languages which can be recognized using Finite State Automaton. Sounds familiar?
Now that we know what formal grammars are, let’s take a closer look at the notations that are used to describe them.
Notation Styles #
There are several different styles of notations for context-free grammars. One of the most widely used is Extended Backus-Naur form (EBNF). It is a combination of standard Backus-Naur Form with an addition of the constructs often found in regular expressions like quantifiers, and some other extensions.
Unfortunately, there is no single EBNF standard. There is a ISO/IEC 14977 standard which defines EBNF, but some people don’t recommend using it. Ultimately, it’s up to which tools are available on your platform/language and which notation they support. I’m going to stick with a W3C notation because it is supported by the tool which I’m going to use to generate railroad diagrams.
History of Backus-Naur Form (Additional Reading)
In the middle 1950s, computer scientists began to design high–level programming languages and build their compilers. The first two major successes were FORTRAN (FORmula TRANslator), developed by the IBM corporation in the United States, and ALGOL (ALGOrithmic Language), sponsored by a consortium of North American and European countries. John Backus led the effort to develop FORTRAN. He then became a member of the ALGOL design committee, where he studied the problem of describing the syntax of these programming languages simply and precisely.
Backus invented a notation (based on the work of logician Emil Post) that was simple, precise, and powerful enough to describe the syntax of any programming language. Using this notation, a programmer or compiler can determine whether a program is syntactically correct: whether it adheres to the grammar and punctuation rules of the programming language. Peter Naur, as editor of the ALGOL report, popularized this notation by using it to describe the complete syntax of ALGOL. In their honor, this notation is called Backus–Naur Form (BNF).
Regex Grammar #
I think we are now ready to define an actual regex grammar! You can start either constructing it bottom-up or top-down, depending on what you prefer. I will start doing it top-down.
The regex begins with an optional Start of String of Line Anchor followed the expression.
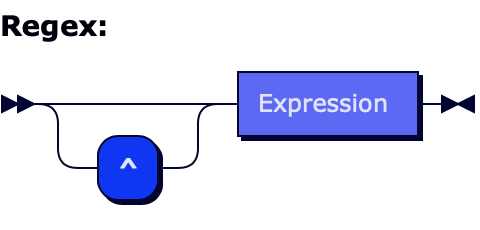
Regex ::= StartOfStringAnchor? Expression
StartOfStringAnchor ::= "^"
Now goes probably the most challenging part. How to define an expression? An expression can be as simple as a single character match. And it can be as complex as multiple nested groups with alternations and quantifiers. Each of these subexpressions can be followed by one another. For example, an expression might start with a single character and can be followed by a group: “a(bc)*”.
Let’s formalize it:
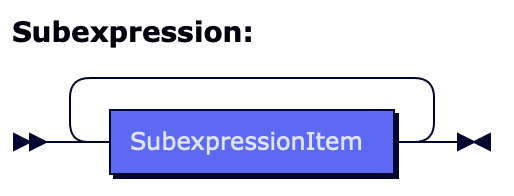
/* Anything that can be on one side of the alternation. */
Subexpression ::= SubexpressionItem+
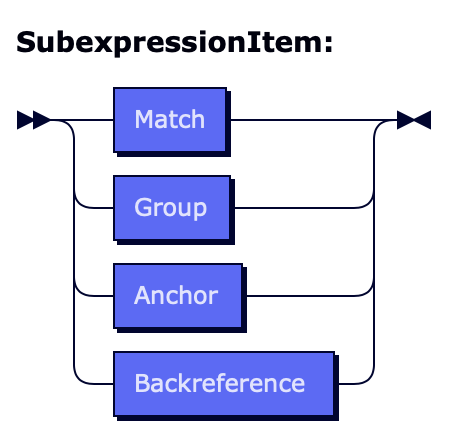
SubexpressionItem
::= Match
| Group
| Anchor
| Backreference
I’m not going to go through all of the possible expression items but here are a few examples. Let’s start with Group. Group is a recursive construct – a group may contain other groups, or actually any subexpression.
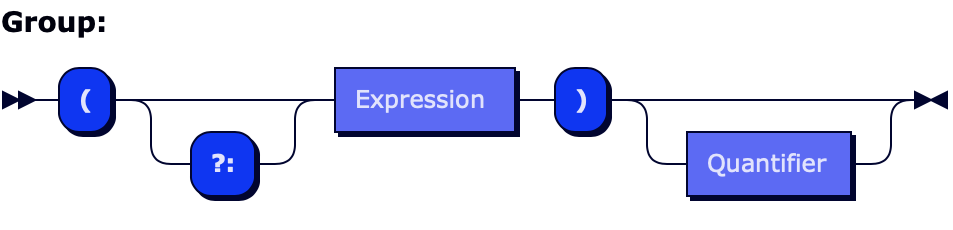
Group ::= "(" GroupNonCapturingModifier? Expression ")" Quantifier?
GroupNonCapturingModifier ::= "?:"
This is the first example where we used recursion. When a parser encounters an opening parentheses, it checks whether the group is Non-Capturing and then parses a subexpression until in encounters a matching closing parentheses.
Note: not all parse generator support indirect recursion like we used here.
I think you get the idea. You can find a complete regex grammar along with a railroad diagram on GitHub.
What’s Next #
In the next article I will write a parser based on the grammar. There are multiple ways to do that. You can write a parser by hand or generate it. A parser can use a top-down or bottom-up approach. You can use parser combinators, etc. I will look at all of these options.
References
- Dick Grune, Ceriel J.H. Jacobs (2008), Parsing Techniques, VU University Amsterdam, Amsterdam, The Netherlands
- Gunther Rademacher, Railroad Diagram Generator
- W3C (2008), EBNF Notation